[Vi] Chiến thuật chơi bạc luôn thắng?

Các trò chơi cá cược từ lâu cuốn hút một lượng lớn người chơi tham gia, nhưng thường kết thúc không có hậu cho con bạc. Xác suất là bộ môn toán học nghiên cứu quy luật, hình mẫu cho các hiện tượng ngẫu nhiên. Liệu có thể dùng xác suất để đòi lại công bằng cho các con bạc hay không? Bài viết này thảo luận một chiến thuật với trò chơi đề.

Chơi đề là một trò chơi đơn giản. Hai số cuối của giải xổ số tạo thành $100$ cặp số từ $00-99$ xuất hiện ngẫu nhiên hằng ngày. Người chơi đặt cược $1$ số, nếu trúng số đó sẽ nhận được $70$ lần tiền cược, nếu thua sẽ mất tiền cược.

Nếu cược đều với số tiền cược M, lợi nhuận kỳ vọng mỗi lần là $P = 700.01M-M = -0.3M$ .Tức là nếu cược ngẫu nhiên 1000 lần (một số lớn), mỗi lần M tiền cược thì bạn sẽ lỗ bình quân 300M.

Nhưng giả sử L là lỗ lũy kế của các lần chơi trước đã xác định, vì nếu trúng bạn sẽ nhận được $70M$, như vậy chẳng phải luôn tồn tại một giá trị $M_{min}$sao cho nếu trúng sẽ bù được toàn bộ phần lỗ L và thậm chí có lãi. Cụ thể, $M_{min}= L/69$.

Như vậy, bằng cách đặt mức tiền cược sao cho tiền thưởng nếu trúng cao hơn và bù được phần lỗ lũy kế, đến một ngày nào đó trúng cược, bạn sẽ bù được toàn bộ phần lỗ và thậm chí có lãi?

Khi đăng chiến thuật này lên diendantoanhoc.org lần đầu, đa số mọi người đều đồng tình mệnh đề này là đúng trên lý thuyết, nhưng số tiền cược có thể tăng theo cấp số nhân và trở nên lớn đến mức không thực tế. Ta sẽ thử tính toán xem giá trị đó có thực sự lớn không.

Hàm lợi nhuận kỳ vọng

Giả sử bạn đặt mục tiêu chiến thắng $e=100$ đồng.

1. Trước hết ta tính toán giá trị tiền cược cần đặt mỗi ngày:
   
   • Trong ngày đầu bạn phải cược ít nhất $M = e/69 = 1.45$ đồng. Nếu trúng, bạn sẽ đạt được mục tiêu và trò chơi kết thúc, nếu trượt, bạn lỗ lũy kế $L = e/69 = 1.45đ$.
     
   • Trong ngày thứ 2, bạn phải cược $M = L/69 + e/69 = e(69^{-1} +69^{-2})$ để nếu trúng, sau khi bù phần lỗ lũy kế bạn vẫn đạt được mục tiêu chiến thắng e đồng
     …
   • Trong ngày thứ $n$, bạn phải cược $M$ và giá trị lỗ lũy kế $L$ (sau khi trượt) lần lượt là:
     $ M = \frac{L}{69} +\frac{e}{69} = \sum_{i=0}^{n-1} C_i^{n-1}69^{-i}e$
     $L = \sum_i^n C_i^n 69^{-i}e$

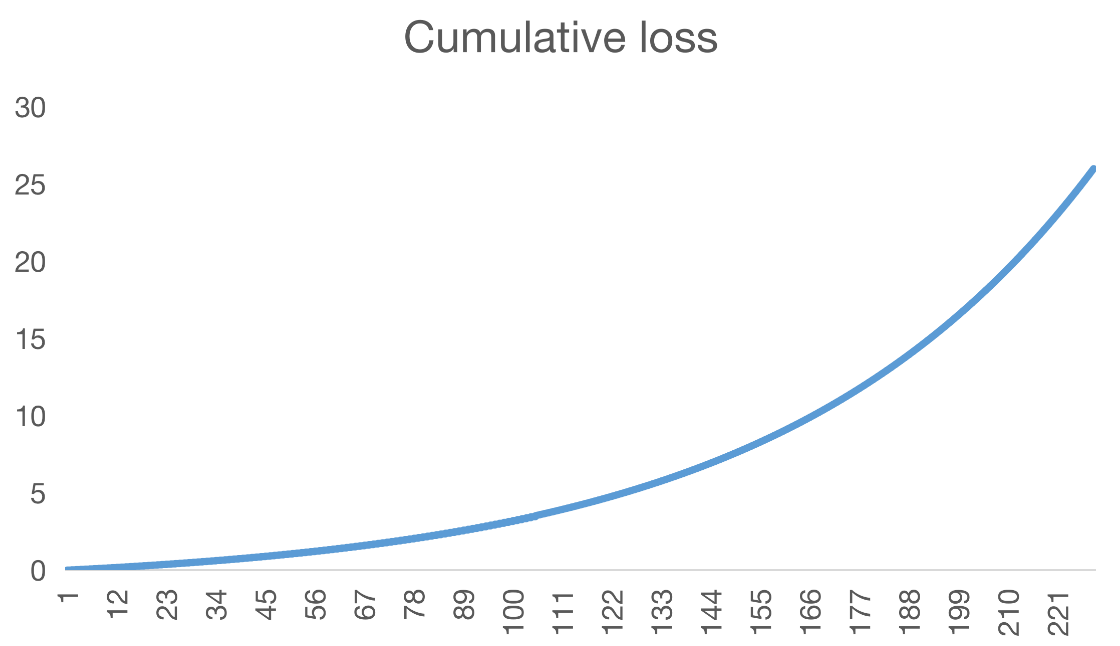
Đồ thị của hàm lỗ lũy kế sau $n$ ngày liên tiếp trượt là:

1. Ta sẽ ước lượng thời gian để bạn trúng số.
   • Trong ngày 1, xác suất để bạn trúng là $p= 0.01$, xác suất đề bạn trượt là $1-p = 0.99$. Nếu trúng, trò chơi kết thúc, vì vậy ta xét tiếp trường hợp bạn trượt.
   • Trong ngày 2, xác suất để nếu bạn trượt trong ngày 1 nhưng trúng trong ngày 2 là $p(1-p)$, xác suất để bạn trượt ngày 1 và tiếp tục trượt ngày 2 là $(1-p)^2$. Tương tự, nếu trúng trò chơi kết thúc nên ta sẽ chỉ xét tiếp trường hợp bạn trượt.
     …
   • Đến ngày n và bạn vẫn chưa trúng, xác suất để bạn trúng là $p(1-p)^(n-1)$.
     => Ta nói hàm phân phối xác suất của biến cố trúng tại ngày thứ n (trong điều kiện những ngày trước trượt) là: $P(X=n) = p(1-p)^{n-1}$

Hàm phân phối tích lũy $F$ tại ngày thứ $n$ xác định bởi:
$F(n) = \sum P(X \leq n) = \sum_{i=1}^nP(X=i) = 1 - (1-p)^n$

Đồ thị CDF và PDF có dạng:

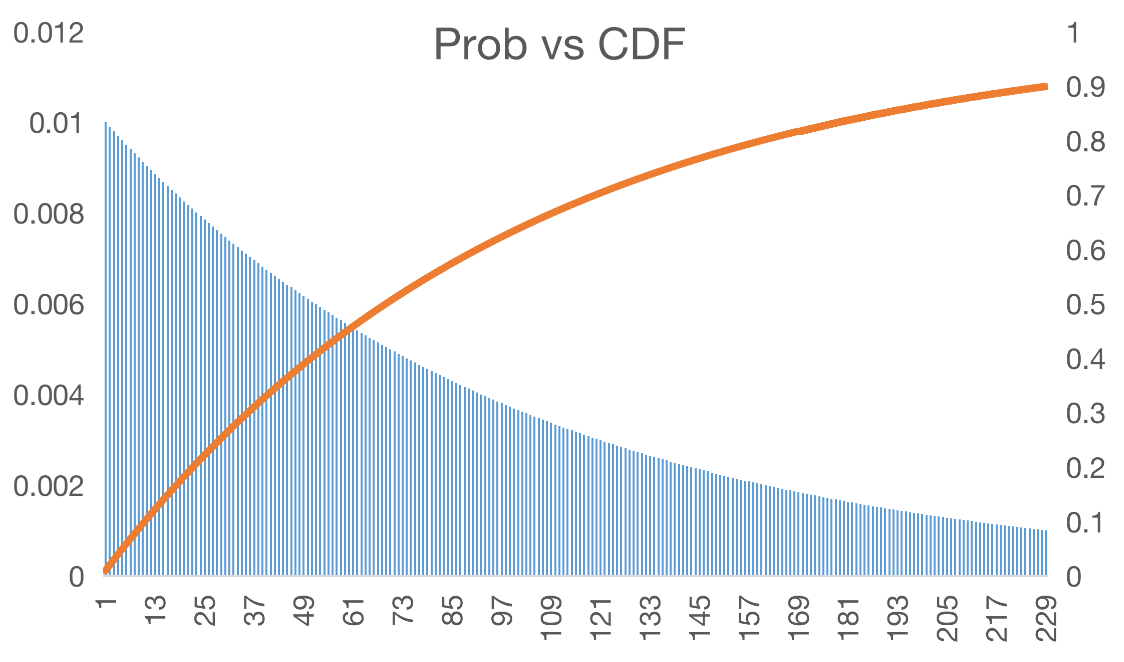
Ý nghĩa của giá trị $F(n)$ là xác suất mà bạn sẽ trúng tại số ngày nhỏ hơn n.
Ta mong muốn một giá trị tương đối chắc chắn đến 90% và muốn biết số ngày cần sẽ cược là bao nhiêu để có thể trúng. Để tìm $n$, ta có $F(n) = 0.9 \Leftrightarrow n \sim 229.$
Như vậy, nếu mỗi ngày đều cược 1 số đề ngẫu nhiên, thì đến 90% trong vòng không quá 229 ngày bạn có ít nhất 1 ngày trúng cược. Điều này nghĩa là bạn phải chuẩn bị một lượng tiền vốn đủ lớn để trong trường hợp xấu nhất ngày 229 mới trúng. Khi đó vốn bạn cần chuẩn bị là:

$I = L(229) = \sum_{i=1}^{229} C^{229}_i 69^{-i}e \approx 25.987e$
Như vậy, bằng việc chuẩn bị gấp 26 lần số tiền lãi mục tiêu và thực hiện chiến thuật tăng đều đặn giá trị tiền cược như mục (1), đến 90% trong vòng không quá 229 ngày bạn sẽ đạt được tiền lãi mục tiêu của mình.

26 lần là con số hoàn toàn khả thi để triển khai trong thực tế. Theo bạn chiến thuật trên có khả thi không?